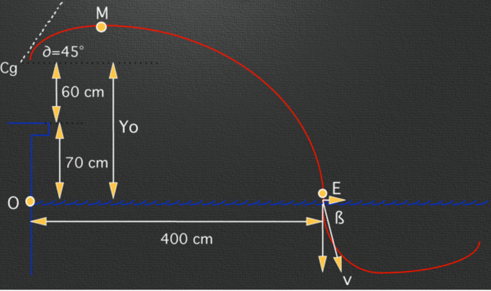
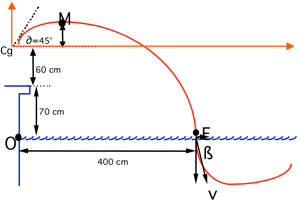
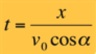Modélisation théorique du plongeon départ


Cette trajectoire correspond à un mouvement uniformément varié.
Dans ce cas:a=gv=gt + vo
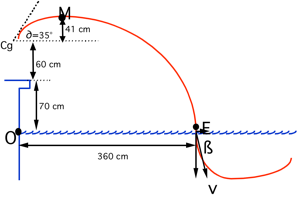
L’origine O se situant à l'intersection de la surface de l'eau et du mur,
OCg= 1/2 gt2 + v0t + y0 (y0 = hauteur OGg)
En se reportant sur l'axe des x (Horizontal) et des y (Vertical) on obtient :
a x=0 v x=voCos a
y= -g y=-gt + voSin a
OCg x=voCos a t
y= - 1/2gt2 + voSin a t + yo
D'où : de x on obtient
Recherche de v0 au départ de la courbe
De l'équation, vo=√ (gx2/(2cos2a(tga x + y0))) on obtient du point E, avec :
x=4 my=0yo =1,3 ma =45°
donc vo= 5,04 m.s-1
Pour éviter les erreurs dues aux approximations des calculs (chiffres arrondis), il faut recalculer la distance exacte du point E :
0 = -0,393 x2 + x + 1,3
Calcul d’une équation du 2e degré : y=ax2+bx+c
∆=b2-4ac
y = (-b-√∆)/2a y’= (-b+√∆)/2a
∆ = 1+(4*0,394*1,3) = 3,049
d = (-1-1,746)/(-0,788) = 3,48 m = x
et donc v0 corrigé est de 5,03 m.s-1
Recherche du temps pour rentrer dans l'eau:
t=x/voCosa
t= 0,97 s
Recherche de la vitesse d'entrée dans l'eau
La vitesse est la dérivée de l'équation de la courbe, donc y = -gt + vo
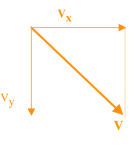
vx=voCosa
vy=-gt + vo Sina
Selon le théorème de Pythagore: v2=vx2 + vy2
vx =3,557
vy = -6,143
donc v2=vx2 + vy2 donc v= 7,10 m.s-1
Recherche de l'angle ß de v en E
Tgß = vy / vx
Tgß = -1,727
ß = -59°92
Point culminant de la courbe (M)
Il suffit de remonter l’Origine au point de départ du Cg
et calculer la distance d de l’intersection entre la courbe et l’axe des x
Mx = d/2
Point culminant de la courbe (M)
En résumé, pour ∂=45° et pour vo=5,03 m.s-1:
d = 3,48 m
t = 0,97 s
vE = 7,10 m.s-1
ß = - 60°2
hM = 1,93m (63 cm des hanches)
pour ∂=35° et pour vo=5,03 m.s-1:
d = 3,61 m
t = 0,85 s
vE = 7,10 m.s-1
ß = - 54°8
hM = 1,71m (41 cm des hanches)
La vitesse d'entrée dans l'eau est identique, quelque soit a initial. En fait, vo se retrouve sur l'autre partie de la parabole sur le plan horizontal. De ce fait, la vitesse d'entrée dans l'eau ne dépend que de la hauteur de Cg par rapport à O et de vo.
3 paramètres restent importants pour cette étude :
le Temps aérien pour des raisons évidentes de chronomètre
la Distance parcourue en l'air afin de limiter la dépense énergétique due à la nage
l'Angle de pénétration dans l'eau qui va avoir une influence sur le maître-couple, et donc sur la résistance.

Le plongeon départ : Paradoxe entre la théorie et la pratique
L'intérêt du départ plongé réside dans le gain de temps induit par sa bonne réalisation, notamment sur les épreuves de sprint. En effet, les faits de s'appuyer sur un appui solide, de réaliser une trajectoire arienne (sans la résistance de l'eau) et enfin de partir de plus haut, sont autant d'éléments qui favoriseront la qualité du plongeon.
Ainsi, à partir de ces éléments, il est relativement simple d'imaginer une trajectoire optimale. Le but serait de rentrer dans l'eau le plus loin possible afin d'éviter les frottements aquatiques, en adoptant une position la plus hydrodynamique possible, à une vitesse la plus importante possible. Les paramètres "temps de réaction" et "mise en action" étant d'un secteur quelque peu différent, ils ne seront pas pris en compte.
Pour essayer de modéliser une trajectoire, la première difficulté est de définir un point de référence. En général, c'est le centre de gravité qui est pris en compte. Cependant, la position des segments corporels n'est pas constante durant le plongeon, ce qui a pour conséquence un déplacement constant du centre de gravité. Ceci étant, la hanche peut être considérée comme un point de référence de par son emplacement proche de cette variation du centre de gravité théorique.
Ainsi, pour aller le plus loin possible, la trajectoire de la hanche devrait s'apparenter à une parabole. La trajectoire devrait donc s'orienter vers le haut à un angle de 45°. Cependant, puisque le plot est plus haut que la surface de l'eau, l'angle de mise en action devrait être inférieur.
Un 2e paramètre entre en ligne de compte : le temps du plongeon. Il n'est pas concevable de prendre trop de temps dans cette phase aérienne. L'objectif est donc d'aller le plus loin en un minimum de temps.
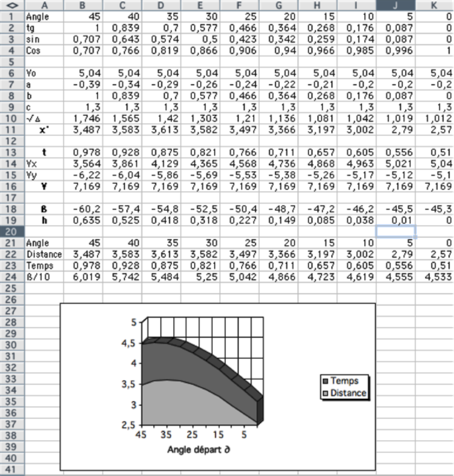
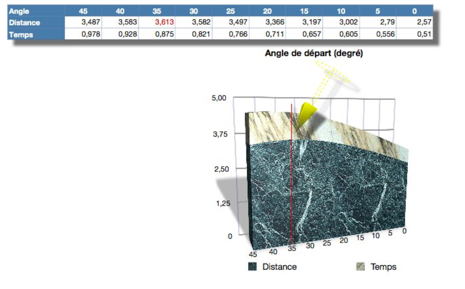
Les calculs mathématiques nous montrent qu'avec une vitesse de départ (lorsque le nageur quitte le plot) de 5m/s et d'un angle de démarrage de 45°, la distance parcourue est de 3,5 m et la durée de vol est de 0,98s. Pour un angle de 35°, la distance parcourue est de 3,6m en 0,87s. Ainsi, si l'on cumul ces 2 paramètres Temps d'envol - Distance parcourue, l'angle de 35° est l'angle optimal théorique puisque le nageur va plus loin en moins de temps.
La vitesse d'entrée dans l'eau est, quel que soit l'angle (la vitesse de début étant identique), de 7,1 m/s. Cette vitesse est nettement supérieure à la vitesse moyenne de nage (7 m/s à 2 m/s). D'autre part, comme il est plus facile de conserver la vitesse plutôt que de la créer (MAGLISCHO). Ceci prouve bien que le départ est le point clé pour le sprint. En effet, il va donc déterminer une vitesse initiale, une bonne pénétration dans l'eau, une reprise de nage efficace, et donc un placement du corps idéal pour limiter la résistance à l'avancement.
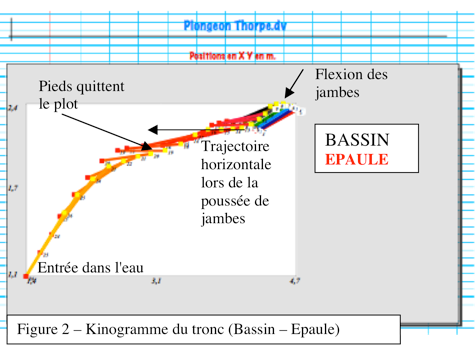
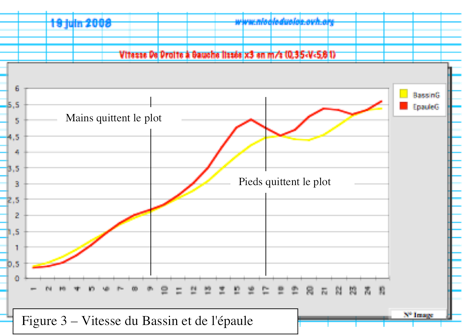
Actuellement, tous les nageurs, de niveau mondial ou inférieur, ne sont pas du tout conformes avec ce modèle. L'exemple de Y. Thorpe résume assez bien ce fait. Son étude montre que la vitesse de son bassin (centre conventionnel de gravité) est d'environ de 5m/s lorsqu'il quitte le plot (figure 3), similaire à l'hypothèse théorique. Pourtant, les résultats suivants sont différents. Il débute en effet, après la flexion des jambes, par une trajectoire horizontale (Figure 2). D'autre part, la distance d'entrée dans l'eau (Figure 2) est inférieure aux résultats mathématiques (3,3m contre 3,6m)
Enfin, la vitesse d'entrée dans l'eau est de 5,5m/s contre 7,1 m/s théorique, et la durée de vol est de 1s (figure 3) contre 0,87s..
Il est donc surprenant de constater que ce nageur a la capacité musculaire pour développer une vitesse de départ importante mais décrit une trajectoire dont les résultats apparaissent limités. Or, via les calculs mathématiques, il suffit de lui demander une modification de trajectoire en passant par-dessus une perche située à 41cm (calculs mathématiques) des hanches (ou 1,01m du plot) afin d'optimiser ses résultats.
Ceci étant, la gestuelle du Grap start semble induire, sans doute intuitivement, une trajectoire horizontale. Les mains accrochées au plot provoquent un abaissement de la tête, contraire à une action vers le haut Peut-être qu'avec un apprentissage spécifique, cette trajectoire peut être corrigée afin de tenter de s'approcher des résultats théoriques plus performants.
Ceci tant donc à démontrer que le modèle théorique et l'existant ne sont pas toujours identiques. Pourtant, une modification des habitudes et des apprentissages pourrait prétendre à faire évoluer la performance. Dans ce cas précis, lorsque Moorhouse réalisait un plongeon exagérément vers le haut pour le départ brasse, tout le monde l'imitait. Aujourd'hui, les différents plongeons semblent privilégier le temps de réaction à la qualité du plongeon en lui-même, peut être à tort.
Frédéric DUCLOS