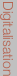Frédéric DUCLOS

CREPS de Bourgogne, Dijon (21)

Le plongeon départ a subi d’énormes évolutions ces 20 dernières années. Les nageurs ont tout d’abord cherché à monter très haut, particulièrement les brasseurs, pour ensuite revenir à un plongeon plus à plat. La position des pieds a aussi évolué en passant par une accroche avec les deux pieds à l’extrémité avant du plot, bras en arrière, puis mains accrochant le plot et enfin pieds décalés, c’est-à-dire, un pied accroché devant et l’autre en appui derrière. Pour compléter cette évolution, le matériel a aussi évolué en implantant un support en bais à l’arrière du plot comme en athlétisme pour les starting blocks.

Afin de comprendre cette évolution, le Centre de Ressource et d’Expertise du CREPS de Dijon a étudié succinctement la théorie mathématique du plongeon en la comparant à des départs plongés réels, sans et avec le starting block.

Explication de l’étude

L’étude théorique se base sur le schéma 1. Le Centre de Gravité (CG) est représenté par la hanche afin de faciliter par la suite l’étude du plongeon réel. Ainsi, il ne s’agirait que d’un simple mouvement uniformément varié dont les formules mathématiques restent malgré tout assez accessibles. De fait, nous pourrions étudier la vitesse du CG lorsque les pieds du nageur quittent le plot (Vo), l’angle de la trajectoire du CG au même moment (A), l’angle de la trajectoire du CG lors de l’entrée dans l’eau (ß), sa vitesse à cet instant (V), la distance aérienne parcourue  (Dist) et le temps correspondant (t). Tous ces indices permettraient à l’entraîneur d’orienter facilement son nageur vers un apprentissage plus précis de cette action motrice.

Les résultats de ces données théoriques montrent que le meilleur compromis temps (t) / Distance aérienne parcourue (Dist) serait obtenu avec un angle de départ (A) de 37° au dessus de l’horizontal (Schéma 2).

Etude pratique

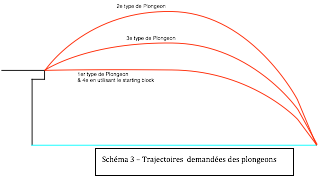
Afin de comparer cette étude théorique avec des cas in situ, 4 types de plongeons ont été étudiés (schéma 3). Le 1er correspond à un plongeon pieds devant et une trajectoire du CG lorsque les pieds quittent le plot proche de l’horizontal. Le 2e correspond à un plongeon, pieds devant, avec une trajectoire d’environ 30°. Le 3e correspond à un plongeon, pieds devant, avec une trajectoire intermédiaire de 15° environ et le 4e correspond à un plongeon utilisant le starting block, donc avec une trajectoire attendue horizontale. Une perche placée à 1,5m devant le plot permet de guider le nageur pour réaliser sa trajectoire.

Pour chacun de ces types de plongeons, 3 essais étaient réalisés. Ainsi, ils seront nommés respectivement « Nom N°type-N°essai ». Pour exemple « F 2-3 » correspond au nageur « F » pour le 2e type de plongeon (vers le haut à 30°) et lors de son 3e essai. Pour les plongeons avec le starting block, ils seront nommés « Nom S-N°essai ».

Un complément à cela : à l’issu des 3 premiers types de plongeons, il a été demandé au nageur de réaliser un plongeon avec l’angle qui lui convenait le mieux. Il est donc dénommé « Nom Choix »

Pour cette étude, 3 nageurs de niveau national ont été sollicités et 2 pour le plongeon avec le starting block (le 3e étant malade lors des essais). Certes, il ne s’agit que d’un très faible échantillon de nageurs mais 36 plongeons ont été malgré tout étudiés. Cela pourrait cependant demander à l’avenir un complément de recherche mais les résultats ne manquent pourtant pas pas de surprises et peuvent déclencher une importante réflexion.

Enfin, et afin d’essayer de garantir la volonté de réaliser un départ efficace, un chrono était pris, pour chacun d’eux, sur 10 m. Le chronomètre se déclenche lorsque que le nageur quitte le plot et s’arrête lorsque sa main arrive à 10m. Certes, ces prises de temps sont manuelles mais les valeurs au 1/10 sec restent fiables.

Concernant le recueil des données, un caméscope posé sur pied à une hauteur de 1,70m, placé à 2,5m du plot et 3,5m du bord du bassin permettait d’avoir un champs incluant le plongeoir et la fin des lignes d’eau à 5m. Ceci avait pour but de pouvoir étalonner fidèlement les mesures. Parallèlement, un logiciel de digitalisation élaboré par mes soins permet de récupérer les vidéo et les découper en images (25 images / sec). Par ce procédé, il était alors possible de cliquer, pour chaque image, sur la hanche, point représentant arbitrairement le CG. La digitalisation de chacun de ces plongeons a donc permis de mettre en évidence la trajectoire du CG, son évolution sur l’axe des x et y, l’évolution de l’angulation de sa trajectoire et l’évolution de sa vitesse.

Résultats concernant les plongeons classiques

Malgré cette population expérimentale restreinte, les résultats sont tout à fait surprenants. Tout d’abord, le 2e plongeon (très haut) a posé un gros problème de réalisation tant sur le plan de la direction de départ, mais aussi lors de l’entré dans l’eau. De grosses difficultés apparaissent de par la gestion de la profondeur de la coulée. Un apprentissage semble de fait nécessaire pour résoudre cette problématique.

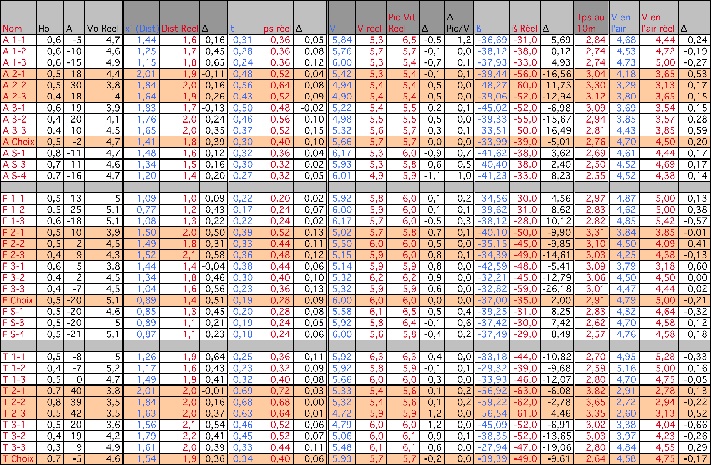
Conjointement, la comparaison théorie/pratique révèle des résultats très incohérents. Le tableau de résultats montre des relevés de Ho, A et Vo Reel recueillis grâce aux résultats de la digitalisation et qui servent de base pour le calcul théorique. Les colonnes en rouge sont aussi issues des relevés de résultats d’observation. Les colonnes bleues sont le résultat du calcul mathématique. ∆ met en évidence la différence entre le calcul et le relevé.

Ainsi, pour le paramètre Dist, les valeurs réelles sont 30cm plus grandes que les valeurs théoriques. Or on aurait pu s’attendre à l’inverse en raison de la résistance de l’air notamment. De plus, 30 cm de différence correspond à une distance de 20% supérieure à la théorie ce qui est très important.

De surcroît, les variations entre les valeurs théoriques et réelles sont totalement anarchiques. Parfois, Dist et Dist Reel montrent une différence de 26cm, parfois de -11cm (plongeons A 2-1 et A 2-3) alors que l’angle A est identique (18°), Ho est sensiblement le même (0,5 et 0,4m) et Vo varie de façon inverse au résultat (4,4m/s pour une distance de 1,9 et 4m/s pour la même distance). Tout ce capharnaüm apparent possède malgré tout un coefficient de corrélation de 0,80, donc une certaine corrélation semblerait persister.

Autrement dit, même si l’on pouvait s’attendre à une différence entre la théorie et la pratique, cette variation aurait due être constante entre les plongeons, ce qui n’est pas le cas. Aucun plongeon n’est véritablement en rapport avec les autres et pour un même plongeon, avec Vo, A et Ho identiques, le résultat final (V, t, ß, Dist) est différent et apparemment aléatoire.

Afin d’essayer de comprendre cette énorme variation et cette anarchie, nous pouvons mettre en avant que la réelle position du CG n’est pas exactement celle de la hanche. De plus le nageur fait varier la position de ses segments tout au long de sa phase aérienne (les jambes se regroupent au point le plus haut, les bras se projettent vers l’avant). Tous ces mouvements parasites modifient donc la position exacte du CG mais pourraient aussi créer une énergie cinétique qui pourrait expliquer ces différences et anarchies de résultats.

Ce discours est le même pour les vitesse d’entrée dans l’eau (V et V réel) et les angles d’entrée dans l’eau (ß et ß reel).
Seuls les temps d’envol (t et t réel) ne varient guère. Du reste, leur coefficient de corrélation est de 0,95 et les variations moyennes sont de 7/100e de seconde.

Quoi qu’il en soit, l’angle idéal théorique de 37° issu uniquement de la théorie du mouvement uniformément variée ne correspond pas à la réalité.

D’autre part, selon les lois simples de la physique, plus je lance un objet haut, plus il retombe vite (à la même vitesse que celle où il quitte ma main). Sachant que le plot est plus haut que la surface de l’eau, cet objet devrait gagner de la vitesse au niveau de l’eau puisqu’il tombe plus bas que son point de départ. Or, les relevés montrent que plonger haut n’implique pas d’augmentation de la vitesse d’entrée dans l’eau (V) et donc, pas d’amélioration du temps au 10m. Pire, un angle de départ (A) important diminue la vitesse de départ Vo. On aurait pu penser que, puisque le nageur a pour consigne d’aller vers le haut, il devrait alors fournir un effort plus important. Dans la réalité, cette vitesse est inférieure, peut être en raison de la pesanteur qui vient en force négative et empêcherait le nageur d’augmenter ou au moins de maintenir une même Vo issue de ses qualités musculaires.

Deuxième axe de remarques.

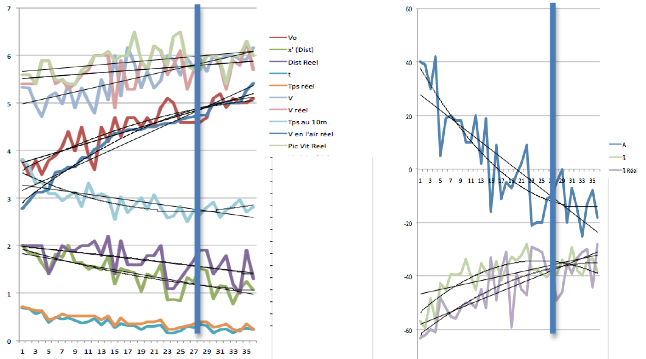
L’incohérence des données en l’état nous empêche d’exploiter au mieux notre expérience. Afin d’essayer de la chuinter nous avons transféré ces données sur un graphe afin d’essayer de lisser les résultats. Ainsi, chaque thème est représenté par une courbe couplée par une courbes de tendance linéaire et polynomiale de degré 2.

De ce fait, plusieurs remarques  apparaissent.

En premier lieu, plus l’angle d’entrée dans l’eau (ß) est fermé (de -27 à -45 environ), plus la performance est bonne. Ceci va de paire avec t réel : plus cet angle ß est fermé, plus le temps d’envol est bref ; mais plus la distance d’entrée dans l’eau (Dist) est courte. Ainsi, nous pourrions en conclure que l’angle fermé  d’entrée dans l’eau (ß) entraine une diminution du temps et de la distance d’envol mais pourrait favoriser la qualité d’entrée dans l’eau au profit de la performance finale.

Les séquences vidéo sous marines montrent en effet, dans cette condition, une quantité moins importante de bulles engendrées par l’entrée du corps dans l’eau. Il y a moins d’éclaboussures (voir pas du tout) ce qui laisse supposer qu’il y a moins de perturbations, donc moins de freins à l’avancement. Ce critère d’éclaboussures pourrait donc être un repère pédagogique pour l’apprentissage.

En second lieu, puisque t et Dist semblent relativement corrélés, pourquoi ne pas les associer. Or associer un temps et une distance induit une vitesse. La partie droite du tableau montre cette vitesse moyenne en l’air, avec les valeurs théoriques et réelles et leur corrélation est des 0,89, soit une bonne corrélation. De plus, la variation moyenne de ces 2 items est nulle (0,00). De fait, cet axe apparaît comme important, et peut être même déterminant.

Globalement, pour une vitesse moyenne importante en l’air (V en l’air), la performance au 10m est meilleure et la vitesse d’éjection du plot (Vo) est plus importante, ce qui semble logique. Parallèlement, une vitesse d’entrée dans l’eau réelle (Vreel) est aussi plus importante, dans cette condition et l’angle de départ (A) est plus fermé (horizontal).

D’autre part, en triant ce tableau sur l’item « V en l’air réel », les indices des courbes polynomiales montrent une déflexion qui se situe aux environs du plongeon n°27, donc un plongeon comportant un angle de départ (A) situé entre -10 et -5°, une vitesse de départ (Vo) d’environ 5m/s.

Bref, ce paramètre semble montrer que pour aller vite dans l’eau, il faut aller vite en l’air. Bien sûr, ceci est une lapalissade, mais compte tenu des expériences passées, notamment lors de l’époque des plongeons vers le haut, cette déclaration n’était pas si évidente.

Ceci étant, pour aller vite en l’air, nous avons précédemment constaté qu’une trajectoire en cloche n’est pas la solution. Donc une trajectoire du CG horizontale et même légèrement orientée vers le bas serait la meilleure façon d’améliorer cette vitesse moyenne en l’air.

En troisième lieu, voici quelques observations que l’on peut mettre en avant lorsque l’on trie les données par rapport à un item particulier.

Ainsi, si l’on trie ces données en fonction de Vo, nous pouvons constater que plus Vo est rapide et moins le nageur va loin, certainement en raison de l’angle de départ A. En revanche, plus Vo est rapide, plus la performance au 10m est bonne ce qui donne des perspectives en termes d’entraînement musculaire.

Si l’on trie ces données en fonction de l’angle de départ (A), nous pouvons constater que quelque soit A, la vitesse d’entrée dans l’eau réelle (VReel) est constante, sauf pour les angles négatifs.

Résultats concernant les plongeons avec starting block

L’utilisation du starting block oblige mécaniquement  le nageur à créer une trajectoire du CG horizontale ou inférieur lors de son éjection du plot. De ce fait, il crée de bonnes conditions pour améliorer cette vitesse moyenne aérienne.

Et pour compléter notre étude, nous avons relevé sur les résultats de la digitalisation issus des observations, les dernières vitesses observables, lorsque le bassin entre dans l’eau. Ceci correspond à 12 à 16/100 plus tard par rapport à notre point de référence. Pour rappel, ce dernier était pointé lorsque les mains du nageur touchaient l’eau, donc situé bien au dessus de la surface de l’eau. ∆ Pic/V correspond à la différence entre les valeurs de cette vitesse des hanches à fleur d’eau (V Pic réel) et la vitesse à notre point de référence (V réel).

En triant les données sur cet item ∆Pic/V, la majorité des valeurs ne montre aucune variation (entre 0 et 0,2m/s). Or, les plongeons utilisant le starting block montrent des variations de 0,4 à 1 m/s. De fait, le passage des bras et du tronc dans l’eau semble moins freiner le nageur avec ce type de départ, et donc, sa vitesse aquatique au début de l’entrée dans l’eau peut gagner jusqu’à 17%.

En harmonie avec ce précédent résultat, ces plongeons obtiennent les meilleures valeurs de performance au 10m, certainement suite aux l’explications précédentes : meilleur vitesse d’entrée dans l’eau et moins de turbulences.

En conclusion

Cette expérience nous montre que la théorie ramenée qu’au simple mouvement uniformément varié est erronée et qu’elle nécessite d’inclure d’autres paramètres. Une étude de la position exacte du CG via un logiciel prenant en compte la longueur, le poids et la position de chaque segment pourrait déjà certainement régler certaines incohérences rencontrées ici. Une mesure plus précise de l’énergie cinétique impliquée par les variations de positions du CG au court de la trajectoire aérienne serait sans doute aussi utile pour comprendre la différence entre V et VReel par exemple.

Cependant, cette étude met en évidence la pertinence de ce nouvel outil qu’est le starting block. Même si son concept pourrait supposer une meilleure Vo, nos résultats ne montrent que les plongeons sans starting block permettent aussi de fortes valeurs de Vo. Nos nageurs n’étant pas accoutumés à l’outil, cette hypothèse laisse alors supposer un apprentissage quant à la poussée des jambes. Etant donnée que les pieds sont décalés et peuvent avoir tous les deux un appui réel (particulièrement le pied arrière), cela suppose que l’impulsion devrait être coordonnée : d’abord le pied arrière puis le pied avant. Dans ces conditions, tout est mis en œuvre pour rendre ce type de plongeon réellement plus efficace que les autres, bien sûr à condition de respecter les observations précédemment faites : améliorer Vo grâce à musculation (explosivité) mais aussi grâce à l’apprentissage de la coordination de la poussée, entrer dans l’eau sans turbulence.

Ceci étant, cette nouvelle vitesse d’entrée dans l’eau va, au début, surprendre les nageurs puisqu’elle suppose un gainage plus important, une modification des repères temporaux et d’espace, liés au timing de la mise en action des jambes et de la reprise de nage.